专为高三考生提供有价值的资讯
当一条直线与平面内的任意直线均保持垂直状态,我们称这条直线与该平面互相垂直。依据判定定理:若一条直线同时垂直于平面内的两条相交直线,则该直线必然垂直于整个平面。

观察图示,直线l同时垂直于平面α内的两条相交直线a与b,现需证明:l⊥α。
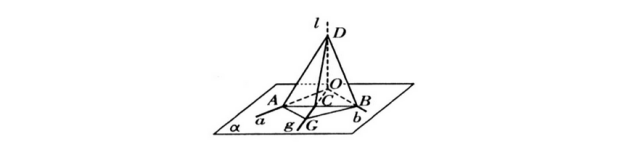
证明:鉴于与a或b平行的直线必然垂直于l,故后续讨论聚焦于那些与a,b均不平行的直线。
首先,将直线a,b以及l平移,使它们相交于同一点O。接着,通过点O绘制任意直线g,并在g上选取一个异于O的点G。然后,过点G分别作GB∥a交b于点B,以及GA∥b交a于点A。连接线段AB,并设AB与OG的交点为C。
由于OA∥GB且OB∥GA,因此四边形OAGB构成平行四边形,从而C为AB的中点。
依据中线定理,我们有OA²+OB²=2OC²+2AC²。在直线l上选取一个异于O的点D,连接DA和DB,再次应用中线定理得到DA²+DB²=2DC²+2AC²。
将两式相减,我们得到DA²-OA²+DB²-OB²=2DC²-2OC²。同时,注意到OD⊥OA且OD⊥OB,因此可以推导出OD²+OD²=2DC²-2OC²,即CD²=OD²+OC²。
由此可得OD⊥OC。由于直线g的选取是任意的,因此直线l与平面α内的任意直线都垂直。
综上所述,我们证明了l⊥α。
1.保定理工学院属于一本还是二本?2025年报考建议及分数线预测
2.保定理工学院分省招生人数及招生专业2025年招生计划参考
8.菱形的判定


2025艺考多少分能上广州珠江职业技术学院 最低分数线是多少
Copyright 2019-2029 http://www.2gaosan.com 【爱高三】皖ICP备18021724号-6
声明: 本站 所有软件和文章来自互联网 如有异议 请与本站联系 本站为非赢利性网站 不接受任何赞助和广告